
| VOLUME 90 (2009) | ISSUE 11 | PAGE 803 |
|---|
|
Non-conformal limit of AGT relation from the 1-point torus conformal block
V. Alba
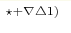 , And. Morozov , And. Morozov  Institute for Theoretical and Experimental Physics, 117218 Moscow, Russia Institute for Theoretical and Experimental Physics, 117218 Moscow, Russia+Landau Institute for Theoretical Physics RAS, 119334 Moscow, Russia ∇Department of General and Applied Physics, Moscow Institute of Physics and Technology 141700 Dolgoprudny, Moscow Reg., Russia  Physical Department, Moscow State University, 119991 Moscow, Russia Physical Department, Moscow State University, 119991 Moscow, Russia Bogolyubov Institute for Theoretical Physics of the National Academy of Sciences of Ukraine Bogolyubov Institute for Theoretical Physics of the National Academy of Sciences of Ukraine03680 Kyiv, Ukraine ID: 11.15.-q, 11.25.Hf
Abstract
Given a 4d 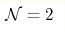 SYM theory, one can construct
the Seiberg-Witten prepotentional, which involves a sum over instantons.
Integrals over instanton moduli spaces require regularisation. For UV-finite
theories the AGT conjecture favours particular, Nekrasov's way of
regularization. It implies that Nekrasov's partition function equals
conformal blocks in 2d theories with WNc chiral algebra
(virasoro algebra in our case).
For Nc=2 and one adjoint multiplet it coincides with a torus 1-point
Virasoro conformal block. We check the AGT relation between conformal
dimension and adjoint multiplet's mass in this case and investigate the large
mass limit of the conformal block, which corresponds to asymptotically free
4d SYM theory, one can construct
the Seiberg-Witten prepotentional, which involves a sum over instantons.
Integrals over instanton moduli spaces require regularisation. For UV-finite
theories the AGT conjecture favours particular, Nekrasov's way of
regularization. It implies that Nekrasov's partition function equals
conformal blocks in 2d theories with WNc chiral algebra
(virasoro algebra in our case).
For Nc=2 and one adjoint multiplet it coincides with a torus 1-point
Virasoro conformal block. We check the AGT relation between conformal
dimension and adjoint multiplet's mass in this case and investigate the large
mass limit of the conformal block, which corresponds to asymptotically free
4d 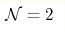 super symmetric Yang-Mills theory. Though technically
more involved, the limit is the same as in the case of fundamental
multiplets, and this provides one more non-trivial check of AGT conjecture. super symmetric Yang-Mills theory. Though technically
more involved, the limit is the same as in the case of fundamental
multiplets, and this provides one more non-trivial check of AGT conjecture.
|
 Home
Home