JETP Letters: issues online

In the framework of simple spin-boson Hamiltonian we study an interplay between dynamic and spectral roots to stochastic-like behavior. The Hamiltonian describes an initial vibrational state coupled to discrete dense spectrum reservoir. The reservoir states are formed by three sequences with rationally independent periodicities 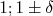$1 ; 1 \pm \delta$ typical for vibrational states in many nanosize systems (e.g., large molecules containing CH₂ fragment chains, or carbon nanotubes). We show that quantum evolution of the system is determined by a dimensionless parameter δ Γ , where Γ is characteristic number of the reservoir states relevant for the initial vibrational level dynamics. When δ Γ > 1 spectral chaos destroys recurrence cycles and the system state evolution is stochastic-like. In the opposite limit δ Γ < 1 dynamics is regular up to the critical recurrence cycle k_c and for larger k > k_c dynamic mixing leads to quasi-stochastic time evolution. Our semi-quantitative analytic results are confirmed by numerical solution of the equation of motion. We anticipate that both kinds of stochastic-like behavior (namely, due to spectral mixing and recurrence cycle dynamic mixing) can be observed by femtosecond spectroscopy methods in nanosystems in the spectral window 10¹¹ - 10¹³ s^-1 .