
| VOLUME 98 (2013) | ISSUE 8 | PAGE 549 |
|---|
|
On the broken time translation symmetry in macroscopic systems: precessing states and off-diagonal long-range order
G. E. Volovik
Low Temperature Laboratory, Aalto University, School of Science and Technology, P.O. Box 15100, FI-00076 AALTO, Finland Landau Institute for Theoretical Physics of the RAS, 119334 Moscow, Russia
Abstract
The broken symmetry state with off-diagonal long-range order (ODLRO), which is characterized by the vacuum expectation value of the operator of creation of the conserved quantum number Q, has the time-dependent order parameter. However, the breaking of the time translation symmetry is observable only if the charge Q is not strictly conserved and may decay. This dihotomy is resolved in systems with quasi-ODLRO. These systems have two well separated relaxation times: the relaxation time τQ of the charge Q and the energy relaxation time τE. If  , the
perturbed system relaxes first to the state with the ODLRO, which persists for a long time
and finally relaxes to the full equilibrium static state. In the limit , the
perturbed system relaxes first to the state with the ODLRO, which persists for a long time
and finally relaxes to the full equilibrium static state. In the limit 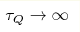 ,
but not in the strict limit case when the charge Q is conserved, the intermediate ODLRO
state can be considered as the ground state of the system at fixed Q with the
observable spontaneously broken time translation symmetry.
Examples of systems with quasi-ODLRO are provided by superfluid phase of liquid
4He, Bose-Einstein condensation of magnons (phase coherent spin precession) and
precessing vortices. ,
but not in the strict limit case when the charge Q is conserved, the intermediate ODLRO
state can be considered as the ground state of the system at fixed Q with the
observable spontaneously broken time translation symmetry.
Examples of systems with quasi-ODLRO are provided by superfluid phase of liquid
4He, Bose-Einstein condensation of magnons (phase coherent spin precession) and
precessing vortices.
|
 Home
Home