JETP Letters: issues online

Two-dimensional potential flow of the ideal incompressible fluid with free surface and infinite depth can be described by a conformal map of the fluid domain into the complex lower half-plane. Stokes wave is the fully nonlinear gravity wave propagating with the constant velocity. The increase of the scaled wave height H/λ from the linear limit H/λ=0 to the critical value 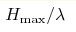$H_{\max}/\lambda$ marks the transition from the limit of almost linear wave to a strongly nonlinear limiting Stokes wave. Here H is the wave height and λ is the wavelength. We simulated fully nonlinear Euler equations, reformulated in terms of conformal variables, to find Stokes waves for different wave heights. Analyzing spectra of these solutions we found in conformal variables, at each Stokes wave height, the distance v_c from the lowest singularity in the upper half-plane to the real line which corresponds to the fluid free surface. We also identified that this singularity is the square-root branch point. The limiting Stokes wave emerges as the singularity reaches the fluid surface. 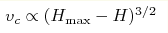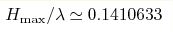From the analysis of data for v_c→ 0 we suggest a new power law scaling $v_c\propto (H_{\max}-H)^{3/2}$ as well as new estimate $H_{\max}/\lambda \simeq 0.1410633$ .