Home
For authors
Submission status

Archive
Archive (English)
Current
   Volumes 113-120
   Volumes 93-112
      Volume 112
      Volume 111
      Volume 110
      Volume 109
      Volume 108
      Volume 107
      Volume 106
      Volume 105
      Volume 104
      Volume 103
      Volume 102
      Volume 101
      Volume 100
      Volume 99
      Volume 98
      Volume 97
      Volume 96
      Volume 95
      Volume 94
      Volume 93
Search
VOLUME 102 (2015) | ISSUE 11 | PAGE 870
Anisotropic characteristics of the Kraichnan direct cascade in two-dimensional hydrodynamic turbulence
DOI: 10.7868/S0370274X15230125
Abstract
Statistical characteristics of the Kraichnan direct cascade for two-dimensional hydrodynamic turbulence are numerically studied (with spatial resolution 8192× 8192) in the presence of pumping and viscous-like damping. It is shown that quasi-shocks of vorticity and their Fourier partnerships in the form of jets introduce an essential influence in turbulence leading to strong angular dependencies for correlation functions. The energy distribution as a function of modulus k for each angle in the inertial interval has the Kraichnan behavior, 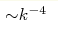{\sim} k^{-4}, and simultaneously a strong dependence on angles. 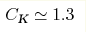However, angle average provides with a high accuracy the Kraichnan turbulence spectrum Ek=CKη2/3 k-3, where η is enstrophy flux and the Kraichnan constant C_{\text{K}}\simeq 1.3, in correspondence with the previous simulations. 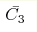Familiar situation takes place for third-order velocity structure function S3L which, as for the isotropic turbulence, gives the same scaling with respect to separation length R and η, S3L=C3η R3, but the mean over angles and time \bar {C_3} differs from its isotropic value.