Home
For authors
Submission status

Current
Archive (English)
Archive
   Volumes 81-92
   Volumes 41-60
   Volumes 21-40
   Volumes 1-20
   Volumes 61-80
      Volume 80
      Volume 79
      Volume 78
      Volume 77
      Volume 76
      Volume 75
      Volume 74
      Volume 73
      Volume 72
      Volume 71
      Volume 70
      Volume 69
      Volume 68
      Volume 67
      Volume 66
      Volume 65
      Volume 64
      Volume 63
      Volume 62
      Volume 61
Search
VOLUME 75 (2002) | ISSUE 3 | PAGE 191
Two-dimensional site-bond percolation as an example of self-averaging system
PACS: 64.60.Cn, 75.10.Hk
Abstract
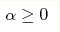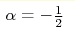The Harris-Aharony for statical model criteria predicts, that if specific heat exponent \alpha \ge 0, then this model does not exhibit self-averaging. In two-dimensional percolation model the index \alpha=-\frac{1}{2}. It means, that in accordance with Harris-Aharony criteria, this model can exhibit self-averaging properties. We study numerically the relative variance RM and Rχ of the probability of site to belong the "infinite" (maximum) cluster M and the mean finite cluster sizes χ. It was shown, that two-dimensional site-bound percolation on the square lattice, where the bonds play role of impurity and sites play role of statistical ensemble, over which the averaging performed, exhibit self-averaging properties.