
| VOLUME 85 (2007) | ISSUE 1 | PAGE 79 |
|---|
|
Local correlations of different eigenfunctions in a disordered wire
M. A. Skvortsov+, P. M. Ostrovsky*+
+L. D. Landau Institute for Theoretical Physics RAS, 119334 Moscow, Russia *Institut für Nanotechnologie, Forschungszentrum Karlsruhe, 76021 Karlsruhe, Germany ID: 73.20.Fz, 73.21.Hb
Abstract
We calculate the correlator of the local density of states 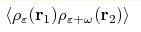 in quasi-one-dimensional
disordered wires in a magnetic field, assuming that in quasi-one-dimensional
disordered wires in a magnetic field, assuming that 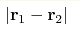 is much smaller than the localization length. This amounts to
finding the zero mode of the transfer-matrix Hamiltonian for the supersymmetric
σ model, which is done exactly by mapping to the three-dimensional
Coulomb problem. Both the regimes of level repulsion and level attraction are
obtained, depending on is much smaller than the localization length. This amounts to
finding the zero mode of the transfer-matrix Hamiltonian for the supersymmetric
σ model, which is done exactly by mapping to the three-dimensional
Coulomb problem. Both the regimes of level repulsion and level attraction are
obtained, depending on 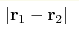 . We demonstrate that the
correlations of different eigenfunctions in the quasi-one-dimensional and
strictly one-dimensional cases are dissimilar. . We demonstrate that the
correlations of different eigenfunctions in the quasi-one-dimensional and
strictly one-dimensional cases are dissimilar.
|
 Home
Home