
| VOLUME 85 (2007) | ISSUE 5 | PAGE 314 |
|---|
|
The density of stationary points in a high-dimensional random energy landscape and the onset of glassy behaviour
Y. V. Fyodorov+∇, H.-J. Sommers*, I. Williams+
+School of Mathematical Sciences, University of Nottingham, NG72RD Nottingham, England *Fachbereich Physik, Universität Duisburg-Essen, D-47048 Duisburg, Germany ∇Petersburg Nuclear Physics Institute RAS, 188300 Gatchina, Leningrad region, Russia ID: 05.40.-a, 75.10.Nr
Abstract
We calculate the density of stationary points and minima of a 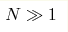 dimensional Gaussian energy landscape. We use
it to show that the point of zero-temperature replica symmetry
breaking in the equilibrium statistical mechanics of a particle
placed in such a landscape in a spherical box of size dimensional Gaussian energy landscape. We use
it to show that the point of zero-temperature replica symmetry
breaking in the equilibrium statistical mechanics of a particle
placed in such a landscape in a spherical box of size
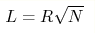 corresponds to the onset of exponential in N
growth of the cumulative number of stationary points, but not
necessarily the minima. For finite temperatures we construct a
simple variational upper bound on the true free energy of the
R=∞ version of the problem and show that this approximation
is able to recover the position of the whole de-Almeida-Thouless
line. corresponds to the onset of exponential in N
growth of the cumulative number of stationary points, but not
necessarily the minima. For finite temperatures we construct a
simple variational upper bound on the true free energy of the
R=∞ version of the problem and show that this approximation
is able to recover the position of the whole de-Almeida-Thouless
line.
|
 Home
Home