
| VOLUME 89 (2009) | ISSUE 8 | PAGE 486 |
|---|
|
Universality and non-universality in behavior of self-repairing random networks
A. S. Ioselevich, D. S. Lyubshin
Landau Institute for Theoretical Physics RAS, 117940 Moscow, Russia Moscow Institute of Physics and Technology, 141700 Moscow, Russia ID: 61.43.-j
Abstract
We numerically study one-parameter family of random single-cluster systems. A finite-concentration topological phase transition from the net-like to the tree-like phase (the latter is without a backbone) is present in all models of the class. Correlation radius index νB of the backbone in the net-like phase; graph dimensions - 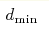 of the tree-like phase, and of the tree-like phase, and 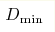 of
the backbone in the net-like phase appear to be universal within
the accuracy of our calculations, while the
backbone fractal dimension DB is not universal: it depends on the
parameter of a model. of
the backbone in the net-like phase appear to be universal within
the accuracy of our calculations, while the
backbone fractal dimension DB is not universal: it depends on the
parameter of a model.
|
 Home
Home